Россия, выключи телевизор (этот зомби-ящик) и думай. Ты уверена, что тебе точно нужна эта нескончаемая сумасшедшая война? Может пора признать за народами право на самоопределение.
Field theory of elementary particles
Introduction to the field theory of elementary particles
(to contents)
It is a translation of articles «Полевая теория элементарных частиц» and «Введение в полевую теорию элементарных частиц» this website with the help the www.translate.ru resource Internet.
I tried to do my best with this text. May be my English is not very good. When I had the possibility to improve my English text, I would replace it.
1. At first we will remember that we authentically know about elementary particles:
(to contents)
- About a half of elementary particles possesses electric charge equal (±е);
- Many elementary particles have the magnetic moment which can be quantized to similarly electric charge;
- Almost all elementary particles have the antiparticles having an opposite sign of electric charge and the magnetic moment;
- Elementary particles possess wave properties;
- Elementary particles didn’t manage to be broken into smaller particles (quarks);
- At collisions of elementary particles other elementary particles are born;
- In interactions of elementary particles there is an element of chance - there is a probability that there will be this or that reaction;
- Elementary particles have such characteristic as backs, something like the rotary moment;
- Elementary particles have quantum characteristics (quantum numbers) - but here it is necessary to be extremely careful as the part of quantum numbers was thought up by the quantum theory, and in their nature cannot be;
- In a microcosm the quantum mechanics, but partially without virtual particles which contradict the law of energy conservation works
- In the nature, so and in a microcosm classical electrodynamics works;
- In elementary particles the special theory of relativity (STR) cannot work.
On it the list can be stopped so far.
2. We will start the analysis
(to contents)
- From this that the part of elementary particles possesses electric charge follows that elementary particles with a nonzero mass of rest have a constant electric field. It can be both the field of elementary electric charge, and dipolar. In the second case elementary electric charge is created by an asymmetric difference of dipolar charges. Existence of dipolar electric field will be coordinated with neutral elementary particles which can possess such field too, but thanks to symmetry of charges at long distances it isn't visible.
- If we want to construct the general theory (both for loaded, and for neutral elementary particles) that exactly dipolar fields best of all are suitable.
- Having entered dipolar electric fields for elementary particles to us automatically (for symmetry reasons) it is necessary to enter also dipolar magnetic fields, and then to unite them in a constant to a component of the electromagnetic field.
Having put all three components in a whole as a result we will receive: in elementary particles there is a variation electromagnetic field from a constant component. And the variation electromagnetic field rotates on a certain radius - we will call it the radius of an elementary particle.
Now for receiving the particles and antiparticles as loaded and neutral we will be forced to enter quantization of polarization of rotation of the electromagnetic field. Namely:
- At rotation of the electromagnetic field in the plane of an electric component charged particle and an antiparticle will turn out (electric charge arises owing to the arisen asymmetry between streams of an external and internal charge);
- At rotation in the plane of a magnetic component (a perpendicular electric component) the neutral particle and an antiparticle will turn out. Here electric charges of dipoles are equal in size, and the difference between particles arises in polarization in relation to the direction a back. If backs it is equal to zero, then it is impossible to distinguish at the macro level a neutral particle from an antiparticle.
At the same time, the elementary particle differs from the antiparticle in polarization of the electromagnetic field. At change of an angle of polarization on π, we will pass from a particle to her antiparticle and vice versa (from an antiparticle to a particle). And at change of an angle of polarization of the electromagnetic field on π/2 we will pass from charged particle (antiparticle) to neutral, and from neutral to load.
The element of chance in behavior of elementary particles is put in the variation electromagnetic field. The result of interaction of elementary particles depends on that what sites of the field of a particle have faced.
Naturally it is necessary to allocate the electromagnetic field with ability to be transformed from one states to others according to laws of the nature. Also electromagnetic field has ability to pass spontaneously to lower power states (with formation of other elementary particles) according to laws of the nature.
3. For receiving a range of elementary particles we will connect quantum mechanics.
(to contents)
We have a distributed electromagnetic weight rotating with velocity of light - therefore, she will have the rotary moment. We will call this rotary moment the internal rotary moment (L) and we will quantize it multiply ħ/2 similar to a back. The set of possible values has turned out:
L = 0; 1/2; 1; 3/2; 2; 5/2; 3...
But according to quantum mechanics this size has 2L+1 more a projection in isotopic space - we have received one more quantum number:
ML = - L; - L+1; ...; L-1; L
The third quantum number of elementary particles needs to be connected with quantization of polarization of rotation of the electromagnetic field. We will call it Q
(the last is entered for difference of a condition of a particle and an antiparticle).
We will enter the formula connecting quantum number L with back (J).
But each elementary particle with L>0 can be and in wild spirits with the additional rotary moment (V). This fourth quantum number of elementary particles can accept the following set of values:
Now it is possible to pass to the most field theory of elementary particles and her postulates.
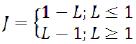
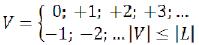
Field theory of elementary particles
The field theory of elementary particles, working within SCIENCE, leans on the base checked by PHYSICS:
- Classical electrodynamics,
- Quantum mechanics (without the virtual particles contradicting the law of energy conservation),
- Conservation laws - are the fundamental laws of physics.
It was necessary to refuse virtual particles: the reasons see (the Virtual particle). Also it was necessary to reject, because of an absence of proof, some quantum numbers postulated by the Quantum theory and Standard model and the conservation laws related allegedly which are unsubstantially attributed by their supporters to number of laws of physics.
The essence of scientific approach of the field theory of elementary particles is consists in it. - The true theory has to work strictly within laws of the nature: the SCIENCE also is consists in it.
Contents:
(to begin)
1. Introduction
(to contents)
Physics of the 20th century, studying elementary particles, I have established existence of the electromagnetic fields following at them:
- constant electric field,
- constant magnetic field,
- electromagnetic field (is variation).
The only elementary particle in the nature possessing only one variation electromagnetic field is the photon moving with velocity of light.
As in elementary particles, with the nonzero size of mass of rest, there is a variation electromagnetic field - which it can only rotate. Here we have also approached the field theory elementary particles. We will the start.
We will take Einstein’s formula (E = m0c2) and we will apply it to one separately taken elementary particle. We will receive that the internal energy concluded is equal to work of mass of rest on a square of velocity of light in an elementary particle. Or translating from mathematical language on language of physics and having remembered that light consists of quanta of the electromagnetic field, we can draw the following conclusion: In an elementary particle there is some distributed weight (we will call it m0~ ≈ m0) rotating with a speed of quantum of the electromagnetic field (c).
If to be exact: in elementary particles the variation electromagnetic field (with a mass of m0~) rotates in which more than 90% of all internal energy - energy of the wave variation electromagnetic field are concentrated (usually). Several percent of total internal energy of elementary particles are concentrated in a constant electric and constant magnetic field of an elementary particle and extend in the space surrounding an elementary particle under laws of Classical electrodynamics.
And time in an elementary particle rotates the mass of m0~ - that there has to be also a rotary moment equal m0~cr (where r - the average radius of rotation). We will quantize it multiply ħ/2 (where ħ - is a Planck constant) and we will consider what particle backs (her rotary moment) can be result of several rotations. Having connected all this with the electromagnetic field and having made on the course of several specifying assumptions as a result it is possible to receive the following.
2. Postulates of the field theory of elementary particles
(to contents)
1. Each elementary particle, except for a photon, is a certain condition of the polarized variation electromagnetic field rotating with velocity of light from a constant component (see fig. 1).
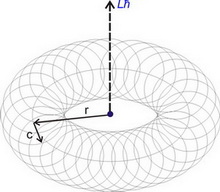
Fig. 1 is a schematic image of an elementary particle.
2. In external environment this field induces the following constant fields:
- quantum electric field (E);
- quantum magnetic field (H);
- external magnetic field of neutral elementary particles (H0) - the field of ring current of radius r=Lħ/m0~c (see item 3).
The mass of rest of an elementary particle (m0), and also the related gravitational field are defined by energy (W) of the sum of this field, including the variation electromagnetic field.
3. To each elementary particle the following three of quantum numbers is unambiguously put in compliance:
L - is the main quantum number - the internal rotary moment of an elementary particle, accepting the following set of values:
L = 0; 1/2; 1; 3/2; 2; 5/2; 3; …
ML - is the quantum number which is responsible for division of particles into subgroups and accepting the following values:
ML = - L; - L+1; … L-1; L - only 2L+1 value;
Q - is the quantum number which is responsible for electric charge and the direction of power lines of a quantum magnetic field of neutral particles (in outside «+0», in inside «-0»):
Splitting on quantum number Q is a consequence of the fact that is possible only four polarization of the electromagnetic field in relation to the internal rotary moment (see fig. 2). Rotation can be carried out or in the plane of an electric component of the field, or in the plane of a magnetic component. In the first case couple of charged particles («particle» and «an antiparticle) differing in a sign of electric charge and a sign of the magnetic moment electric will turn out (to tell more precisely and magnetic water). In the second case couple of neutral particles differing in a sign of a magnetic field and a sign of dipolar electric field will turn out.
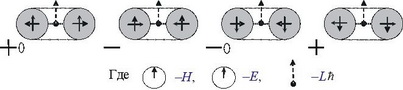
Fig. 2 is the cross section of elementary particles (4 options of polarization).
External manifestation of the internal rotary moment (L) is backs (J) of an elementary particle connected with the L following ratio
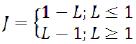 (2)
In turn, the internal rotary moment of an elementary particle is equal
From here
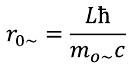 (3)
Thus, «r0~« can be considered as the average radius of rotation of the variation electromagnetic field and «with» as the average linear speed equal by determination of velocity of light. We will call «r0~« the radius of an elementary particle.
Usually, it is accepted to call the main conditions of elementary particles just elementary particles. As we see, the range of elementary particles (their main states) is defined by simultaneous action of Quantum mechanics (distribution of elementary particles to groups and subgroups) and Classical electrodynamics (distribution to the loaded and neutral elementary particles, and also distribution to «particles» and «antiparticles»).
4. Elementary particles with L>0 can be and in wild spirits, different from the basic existence of the additional rotary moment (V). The additional rotary moment (V) is multiple ħ, is the fourth quantum number and can accept the following set of values:
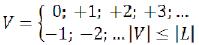 (4)
Where V = 0 means that the particle is in the basic (unexcited) a state, the sign «+» means that the directions of the additional rotary moment and the internal rotary moment coincide, and the sign «-» means that their directions are opposite.
Thus, backs of the excited condition of an elementary particle differs from a back of the main state and it is equal
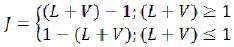 (5)
The excited state the back has other values, the mass of rest, the magnetic moment, time of life and him can be taken for other particle. As we see, the range of the excited states repeatedly duplicates a range of the main conditions of elementary particles.
The elementary particle can pass into the excited state as a result of collision with other particles. After certain time the elementary particle will pass into states with smaller energy (perhaps including in the main state) according to point 5.
5. All transitions (reactions) between elementary particles, irrespective of their state - the basic or excited, are carried out by means of other elementary particles and submit to conservation laws of energy, an impulse, a back (the rotary moment), and also to laws of the electromagnetic field as they are electromagnetic processes. As laws of the electromagnetic field we will take the modified Maxwell’s equations.
where j - is creates the magnetic fields of elementary particles.
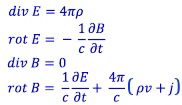
Here j reflecting the fact that the magnetic field arises not only owing to the movement or change of electric field is added to the last equation.
Character and speed of course of transition (reaction) of elementary particles are defined by a condition of variation electromagnetic fields of the participating particles, and also conditions in which these particles are. Influencing an elementary particle it is possible to accelerate or slow down this or that transition.
So, in the base of the field theory of elementary particles lie quantum mechanics (without virtual particles) and classical electrodynamics supplementing each other. It was necessary to refuse virtual particles as they deny operation of laws of the nature and by that contradict classical electrodynamics. What the nature has found instead of virtual particles, it will be visible in the second part of the theory.
3. Range of elementary particles and their states
(to contents)
All elementary particles are subdivided into groups on quantum number L, constant in group.
In turn, each group is subdivided on 2L+1 subgroup on quantum number ML.
In each subgroup with L>0, with the set quantum number V, is exists the two power levels differing in existence of electric charge.
Each power level is split on two conditions of «particle» and «antiparticles» differing in a sign of electric charge or a sign of the magnetic moment. Only power levels with L=1 and Q=0 as because of zero the back a sign of the magnetic moment (μL) and the electric dipolar field becomes uncertain aren’t subject to splitting are π0, K0 and η0 meson.
The fragment of a range of the main conditions of elementary particles (quantum number V=0) is given in fig. 3
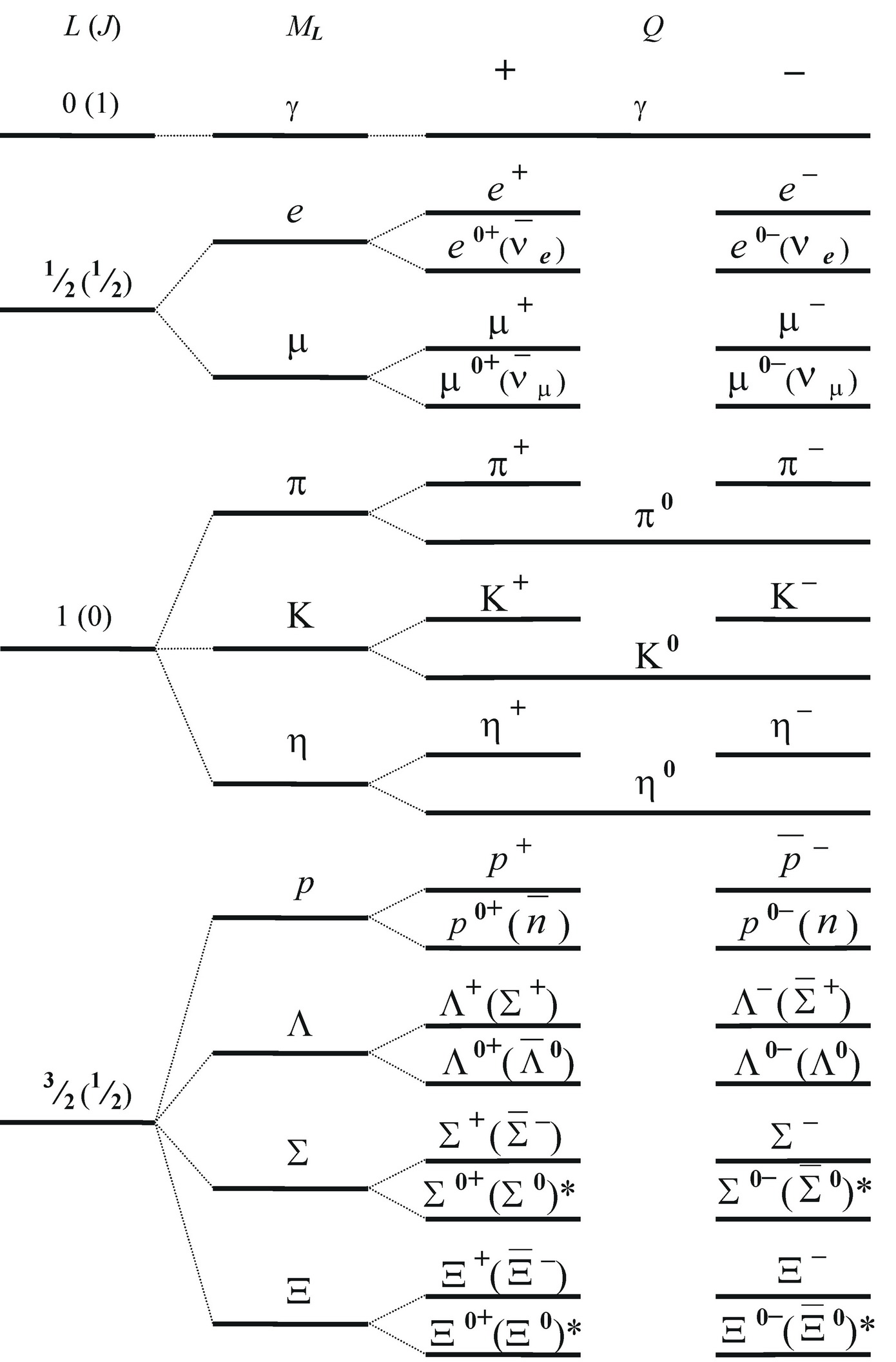
Fig. 3 Fragment of a Range of the Main Conditions of Elementary Particles (quantum number V=0).
The symbol * has marked elementary particles which sign of the magnetic moment isn’t established yet.
As historical names of particles often don’t correspond to the theory, in drawing at first designation of a power level appropriate to a particle (following from the theory), and then in brackets the historical name of a particle is given (if it differs).
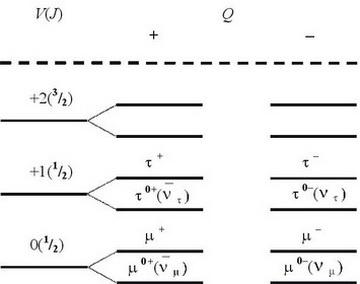
Fig. 4 is of the conditions of subgroup of a muon (μ).
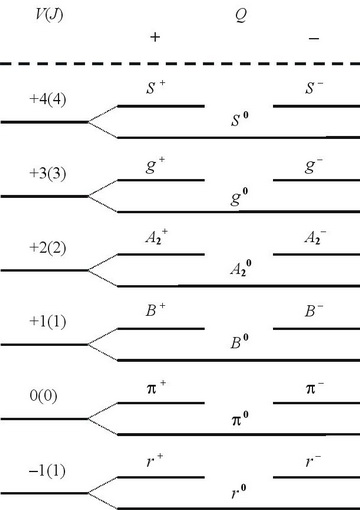
Fig. 5 is of the condition of subgroup π - a meson.
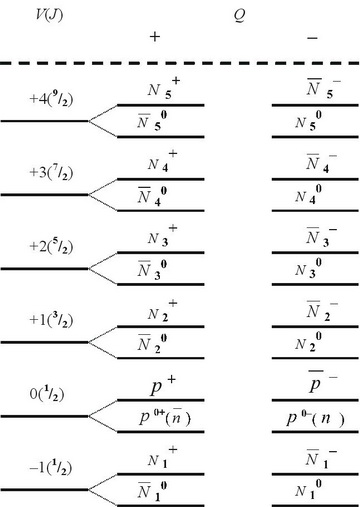
Fig. 6 is of the condition of subgroup of a proton (р).
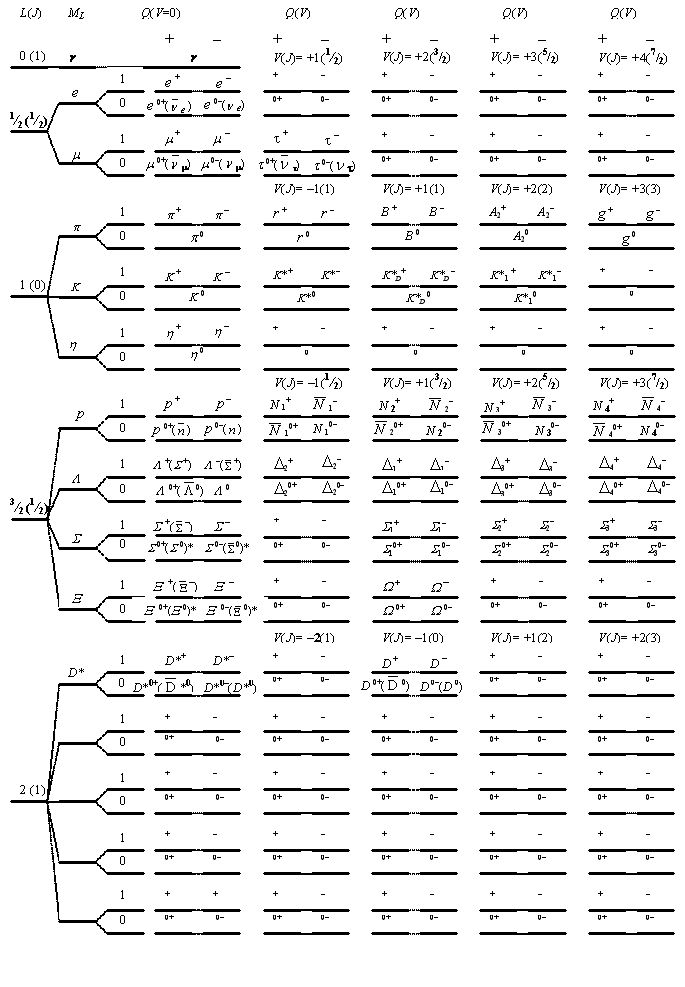
Fig. 7 Fragment of a Range of conditions of elementary particles.
4 Radius of an elementary particle
(to contents)
Radius of an elementary particle with quantum number L>0 (the distance from the center of a particle to the place in which is reached the maximum density of weight) in point (3) has been determined how:
Therefore, the radius of area of the space occupied by an elementary particle is determined by a formula:
A radius more of the ring area occupied by the variation electromagnetic field of an elementary particle was added to the size r0~. It is necessary to remember that the part of size of the mass of rest concentrated in constants (electric and magnetic) fields of an elementary particle is outside this area, according to laws of electrodynamics.
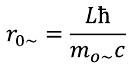
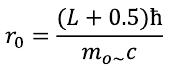
5 Mass of rest of an elementary particle (consequence of Classical electrodynamics)
(to contents)
According to classical electrodynamics and Einstein’s formula, the mass of rest of elementary particles with quantum number L>0 including electron, is defined as an equivalent of energy of their electromagnetic fields:
where a certain integral is undertakes on all electromagnetic field of an elementary particle, E - intensity of electric field, H - intensity of a magnetic field. Here all components of the electromagnetic field are considered: constant electric field, constant magnetic field, variation electromagnetic field.
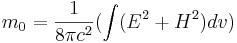
As appears from the given formula, the size of mass of rest of an elementary particle depends on conditions in which she is. Having so placed an elementary particle in constant external electric field, we will affect E2 that will be reflected in the mass of a particle. The similar situation will arise when placing an elementary particle in a constant magnetic field.
6 Electric field of an elementary particle
(to contents)
Constant electric field of elementary particles with quantum number L>0, as loaded, and neutral, is created by a constant component the electromagnetic field of the corresponding elementary particle. And the field of electric charge results from existence of asymmetry between the external and internal hemispheres generating electric fields of opposite signs.
For the loaded elementary particles in a distant zone the field of elementary electric charge is generated, and the sign of electric charge is defined by a sign of the electric field generated by an external hemisphere. In a near zone this field has difficult structure and is the dipolar, but dipolar moment it has no.
Despite zero electric charge of neutral elementary particles (with quantum number L>0), at them has to be constant electric field. The electromagnetic field of which the elementary particle consists (with quantum number L>0) has a constant component, and, therefore, she has to have a constant magnetic field and constant electric field. As electric charge is equal to zero that constant electric field will be dipolar. That is at a neutral elementary particle (with quantum number L>0) has to be constant electric field similar to the field of two distributed parallel electric charges equal in size and an opposite sign. At long distances this electric field will be almost imperceptible because of mutual compensation of fields of both signs of a charge. But at distances, an order of radius of an elementary particle, this field will have significant effect on interactions with other elementary particles close by the sizes.
6.1 Electric field of the loaded elementary particle
(to contents)
For the approximate description of constant electric field of the loaded elementary particle as systems of dot charges, not less than 6 «quarks» in an elementary particle will be required - better if to take 8 «quarks», and at the same time it isn’t important at all, there will be it a positron, π+ meson, a proton, positively charged vector meson, or any other positively charged elementary particle (for negatively charged elementary particles, the field changes the sign, for opposite). Three fantastic quarks in a proton and two fantastic quarks in loaded to the meson can’t display real structure of constant electric field of the loaded elementary particle. Clear business that it is beyond standard model – is a model of quarks.
At any loaded elementary particle, it is possible to allocate two electric charges and respectively two electric radiuses.
For a negatively charged elementary particle:
- the electric radius of external constant electric field (a charge - 1.25e) is - rq-.
- the electric radius of internal constant electric field (a charge +0.25e) is - rq+.
For a positively charged elementary particle
- the electric radius of external constant electric field (a charge +1.25e) is - rq+.
- the electric radius of internal constant electric field (a charge - 0.25e) is - rq-.
Sizes of radiuses are defined by the field theory of elementary particles.
These characteristics of electric field of the loaded elementary particle correspond to distribution of 1 field theory of elementary particles. The physics still experimentally hasn’t established the accuracy of this distribution and what distribution most precisely corresponds to real structure of constant electric field of the loaded elementary particle in a near zone.
Electric radius specifies average location of the electric charge which is evenly distributed on a circle creating similar electric field. Both electric charges lie in one plane (the plane of rotation of the variation electromagnetic field of an elementary particle) and have the general center coinciding with the center of rotation of the variation electromagnetic field of an elementary particle.
Intensity E electric fields of a negatively charged elementary particle (for example, an electron) in a near zone (r ~ r0~), in the SI system as the vector sum, is approximately equal:
where n-=r-/r - is a single vector from near (1) or distant (2) points of a charge of q- of an elementary particle in the direction of a point of supervision (A), n+ =r+/r - is a single vector from near (1) or distant (2) points of a charge of q+ an elementary particle in the direction of a point of supervision (A), r - is the distance from the center of an elementary particle to a supervision point projection to the plane of an electron, q- - is the external electric charge - 1.25e, q+ - is the internal electric charge +0.25e, are highlighted a vector, ε0 - is an electric constant, z - is the height of a point of supervision (A) (distance from a supervision point to the plane of an elementary particle), r0 - is the normalizing parameter. (In the Gaussian unit system there is no multiplier  .) For determination of intensity of electric field of a positively charged elementary particle (for example, a proton), in the equation it is necessary to replace all signs of electric charges with opposite.
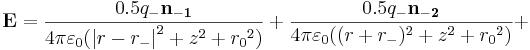
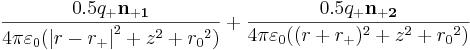
This mathematical expression represents the sum of vectors and it should be calculated by rules of addition of vectors as this field of two distributed electric charges (q-= - 1.25e and q+ = +0.25e). The first and third composed the second and fourth correspond to near points of charges, - distant. This mathematical expression doesn’t work in the internal (ring) area of the elementary particle generating her constants of the field (at simultaneous performance of two conditions: r < ħ/m0~c and Z < ħ/2m0~c).
Potential of electric field of a negatively charged elementary particle (for example, an electron) in a point (A) in a near zone (r ~ r0~), is approximately equal in the SI system:
where r0 - is the normalizing parameter which size can differ from value in a formula E. (In the Gaussian unit system there is no multiplier .) This mathematical expression doesn’t work in the internal (ring) area of the elementary particle generating her constants of the field (at simultaneous performance of two conditions: r < ħ/m0~c and Z < ħ/2m0~c). For determination of potential of electric field of a positively charged elementary particle (for example, a proton), in the equation it is necessary to replace all signs of electric charges with opposite.
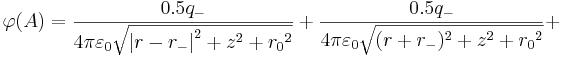
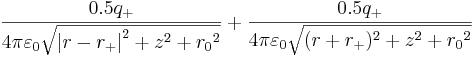
Calibration of r0 needs to be made for both expressions of a near zone on border of the area generating constant fields of an electron.
6.2 Electric field of a neutral elementary particle
(to contents)
Any elementary particle with quantum number L>0 possesses dipolar electric field. In case of a neutral elementary particle including an electronic or muonic neutrino (L=1/2), it will be electric field of two distributed parallel symmetric ring electric charges (+0.75e and - 0.75e), the average radius of re (determined by the field theory of elementary particles) located at distance Average distance  .
The electric dipolar moment of a neutral elementary particle (for example, a neutron, or both neutrinos) is equal:
where ħ - is a Plank constant, L - is the main quantum number in the field theory of elementary particles, e - is an elementary electric charge, m0 - is the mass of rest, m0~ - is the mass of rest concluded in the variation electromagnetic field with - the velocity of light, P - is a vector of the electric dipolar moment (it is perpendicular the planes of an elementary particle, passes through the center of a particle and it is directed towards positive electric charge), s - is the average distance between charges, re - is the electric radius of an elementary particle.
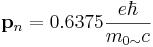
As you can see, electric charges are close in size to charges of estimated quarks (+2/3e= +0.666e and - 2/3e=-0.666e) in a neutron, but unlike quarks, electromagnetic fields in the nature exist, and similar structure of constant electric field any neutral elementary particle, irrespective of size a back possesses and....
Capacity of the electric dipolar field of a neutral elementary particle (for example, a neutron) in a point (A) (in a near zone 10s > r > s approximately), is equal in the SI system:
where θ - is a corner between a vector of the dipolar moment of P and the direction on a point of supervision And, r0 - is the normalizing parameter determined by the field theory of elementary particles is proportional to Lħ/(m0~c), ε0 - is an electric constant, r - is the distance from an axis (rotation of the variation electromagnetic field) of an elementary particle to a point of supervision And, h - is the distance from the particle plane (passing through her center) to a point of supervision And, he - is the average height of an arrangement of electric charge in a neutral elementary particle (it is equal 0.5s), |... | - is the module of number, Pn - is the size of vector Pn. (In the Gaussian unit system there is no multiplier .)
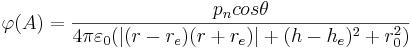
Intensity E electric dipolar fields of a neutral elementary particle (for example, a neutron) (in a near zone 10s > r > s approximately), is equal in the SI system:
where n=r/| r | - is a single vector from the center of a dipole in the direction of a point of supervision (A), (•) - is the designated by a point a scalar product, are highlighted a vector in bold type. (In the Gaussian unit system there is no multiplier .)
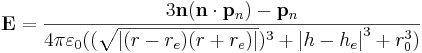
Components of intensity of the electric dipolar field of a neutral elementary particle (for example, a neutron) (in a near zone 10s > r > s approximately) longitudinal (| |) (lengthways radius vector, carried out from a dipole to this point) and cross (_ | _) in the SI system:
where θ - is a corner between the direction of a vector of the dipolar moment Pn and radius vector in supervision point (in the Gaussian unit system there is no multiplier ).
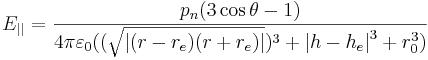
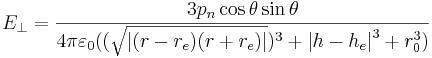
The third a component of intensity of electric field - orthogonal the plane in which the vector of the dipolar moment of Pn of an elementary particle and radius vector lie - is always equal to zero.
Potential energy U interactions of the electric dipolar field, for example, of a neutron (n) with the electric dipolar field of other neutral elementary particle (2) in a point (A) in a distant zone (r >>s), is equal in the SI system:
where θn2 - is a corner between vectors of the dipolar electric moments of Pn and P2, θn - is a corner between a vector of the dipolar electric moment of Pn and a vector of r, θ2 - is a corner between a vector of the dipolar electric moment of P2 and a vector of r, r - is a vector from the center of the dipolar electric moment Pn in the center of the dipolar electric moment P2 (in a point of supervision And). (In the Gaussian unit system there is no multiplier .)
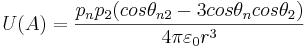
The normalizing r0 parameter is entered for the purpose of reduction of a deviation of value E, from calculated by means of classical electrodynamics and integral calculus in a near zone. The normalization happens in the point lying in the plane of the parallel plane of a neutron remote from the center of a neutral elementary particle on distance (in the particle plane) r0~ and to shift on height on h= ħ/2m0~c, where m0~ - is the size of the weight concluded in the variation electromagnetic field of the based elementary particle (for neutron m0~= 0.95784 m0, and for an electronic neutrino m0~= 0.9776 m0). For each equation the r0 parameter pays off independently. As approximate value it is possible to take field radius:
Follows from all aforesaid that the electric dipolar field of neutral elementary particles (about which existence in the nature, the physics of the 20th century didn’t guess, or I attributed to fantastic quarks), according to laws of classical electrodynamics, will interact with the loaded elementary particles.
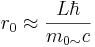
7 The Field theory and theory of gravitation of elementary particles
(to contents)
The field theory of elementary particles was a missing brick of the base in the building of the theory of gravitation of elementary particles.
The following equations of intensity of a gravitational field of the free based elementary particle have been found in the theory of gravitation of elementary particles:
where:
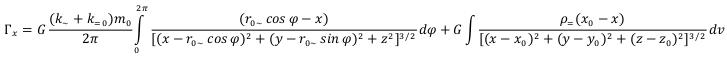
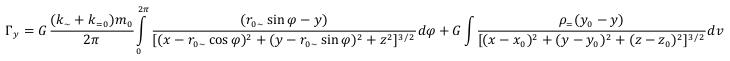
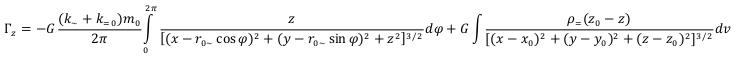
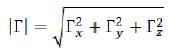
r0~ - is the radius of an elementary particle (average distance from the center of an elementary particle on which the mass of the rotating variation electromagnetic field is concentrated);
m0~ - is the weight concluded in the variation electromagnetic field;
m=0 - is the mass of a constant electric and constant magnetic field concluded in ring area;
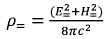 - is the density of substance of a constant electric and constant magnetic field outside ring area;
It has been confirmed that the electromagnetic field mass of elementary particles not only creates their gravitational fields, but also is the reason of their inertial properties.
8 The field theory of elementary particles - Consequences:
(to contents)
The submitted theory isn’t purely classical as the quantum mechanics and classical electrodynamics - supplementing each other lie in the base of the field theory of elementary particles. This theory doesn’t contradict experimental data about fields of elementary particles (except of course fantastic) and at the moment is the only theory describing all range of elementary particles. She explains the mechanism of education and quantization of electric charge, the nature and nature of nuclear interactions on which distances they arise the abnormal magnetic moments of a proton and neutron and many other things. But weeding the equations still it is necessary to write - only some new restrictions for the equations are received.
The microcosm is the world of dipolar constants of electric and magnetic fields and the variation electromagnetic field. At long distances neutral elementary particles behave as the elementary particles which aren’t possessing electric fields. But in a near zone there are powerful fields with a certain structure. And the loaded elementary particle has an area with opposite electric charge inside.
9 New physics: The field theory of elementary particles - the Result
(to contents)
The field theory of elementary particles, working within current laws of the nature, I have found scientific answers to the following questions:
- Why elementary particles possess not only corpuscular, but also wave properties
- What elementary particles consist of?
- From where the mass of rest of elementary particles undertakes and what it consists of
- As there is electric charge of elementary particles and why it is quantized
- As constant magnetic fields of elementary particles are formed
- What is represented by fields of elementary particles in a near zone
- What true sizes of elementary particles
- What is the cornerstone of the mechanism of probabilistic behavior of elementary particles?
- What range of elementary particles and their excited states?
- What are nuclear forces?
- What fundamental interactions really exist in the nature?
- I have brought closer to understanding that it backs
- Why almost all elementary particles are unstable
- The laws existing in a microcosm
- I have allowed rejecting a number of mistakes and delusions of physics of the twentieth century.
By means of the field theory of elementary particles have been made: interesting opening in the field of physics of a neutrino, microwave background space radiation, red shift, the natural simulator of «Dark matter», a power source of Earth proceeding from a subsoil and other planets is found, the first part of the theory of gravitation of elementary particles of which all substance of the Universe consists is constructed, the tale about «Black holes» is sent to archive, the tale about «Big Bang» is buried. How many it will be still made opening in New physics - physics of 21 centuries, time will show.
Knowledge of physics of electromagnetism has considerably changed for the last 150 years.
- Was considered 150 years ago that electric fields are created by electric charges, and magnetic fields as are created by electric currents and can create electric currents.
- After emergence of the equations of Maxwell of the physicist I have established a possibility of independent existence in the nature of the electromagnetic field in a wave mode.
- In the twentieth century of the physicist I have established existence in the nature of electric and magnetic fields independently, irrespective of electric charges and currents.
- At the beginning of the 21st century (in 2010) the physics has established that electromagnetic fields of elementary particles generate fields of charges and currents: the prime causes of electromagnetism are not charges and currents as it was considered in the 19th century - and electromagnetic fields.
- In 2015 the physics has established (though it have been suggested hundred years ago) that electromagnetic fields still create gravitational fields of elementary particles and their inertial weight (see the Theory of gravitation of elementary particles), having confirmed thereby that «Elementary particles of which Universe substance consists - are a form of electromagnetic field matter».
(to begin)
Physics 21 century:
Errors in the physics of the 20th century
Elementary particles (physics)
Gravitation theory of elementary particles
Gravitation theory of elementary particles 2
Gravitation field of elementary particles
Field theory of elementary particles
Fundamental interactions
Vladimir Gorunovich
|
Новая физика - физика 21 века
