Gravitation theory of elementary particles
It is a translation of article “Теория гравитации элементарных частиц” this website with the help the www.translate.ru resource Internet.
I tried to do my best with this text. May be my English is not very good. When I had the possibility to improve my English text, I would replace it.
Contents:
1. Introduction to the gravitation theory of elementary particles
1.1. The base of the gravitation theory of elementary particles
1.2. The gravitational field created by elementary particles
1.3. Choice of units system
1.4. Introduction to the gravitation theory of elementary particles - a result
2. The gravitational field of the elementary particle with a quantum number L>0 (except a photon)
3. The gravitational field of an annular domain (elementary particle)
4. The gravitational field created by an annular domain of the free not moving elementary particle beyond its limits
5. Components of the gravitational field created by an annular domain of the free not moving elementary particle beyond its limits
6. The gravity potential of the field created by an annular domain of the free not moving elementary particle beyond its limits
7. Nature of inertial properties of the elementary particles (electromagnetic nature)
8. The field of a gravitational dipole
8.1. The field of the rotating gravitational dipole, its gravity waves
8.2. Field of an oscillating gravitational dipole, its gravity waves
9. The gravity waves created by thermal agitation a crystal lattice of atoms
10. The gravity waves of the elementary particles
11. Gravitational waves, black holes, and LIGO (Laser Interferometer Gravitational-Wave Observatory).
1. Introduction to the gravitation theory of elementary particles
Physics of the 20th century, studying elementary particles, established existence of the electromagnetic fields in them:
The elementary particle in the nature possessing only one variable electromagnetic field is the photon moving with velocity of light.
Also the physics has established presence at elementary particles the gravitational field.
In elementary particles there is a variable electromagnetic field that has to rotate with the average speed equal to velocity of light.
Here we have approached the field theory of elementary particles, those elementary particles which create gravitational fields of the Universe. This theory is required still more than once.
We will pass to gravitation.
1.1. The base of the gravitation theory of elementary particles
In the base of the gravitation theory of elementary particles are:
The gravitation theory of elementary particles doesn't introduce nonexistent particles and interactions in the nature and doesn't operate laws of the nature. - The essence of scientific approach of the gravitation theory of elementary particles consists in it.
1.2. The gravitational field created by elementary particles
So, let we have an elementary particle with the electromagnetic fields which are (listed above) and a gravitational field. The fantastic fields which are thought up by fantastic theories we will leave them to authors.
According to classical electrodynamics, for this electromagnetic field it is possible to write down the energy density equations. Further calculations will be kept in the Gaussian unit system accepted in classical electrodynamics and convenient for understanding of physics. The interested persons can transfer the equations in to SI independently.
Density of the electric field energy (both constant and variable) will be:
Similarly, density of the magnetic field energy (both constant, and variable) will be: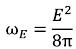 (I-1)
(I-1)
Where E - is the electric field intensity, H - is the magnetic field intensity.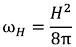 (I-2)
(I-2)
According to the law of conservation of energy, both the energy densities can be put together and as a result we will receive density of the electromagnetic field energy of an elementary particle:
The electromagnetic field energy of an elementary particle (we will designate her as W0), according to integral calculus, is defined: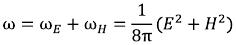 (I-3)
(I-3)
Where the definite integral is undertakes on all space occupied by the electromagnetic field of an elementary particle.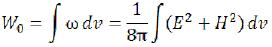 (I-4)
(I-4)
Having used Einstein’s formula, we, on the one hand, will receive the equation of the rest mass of an elementary particle:
and on the other hand we will receive density of the weight (“substance”) of an elementary particle (which will be required for to us further):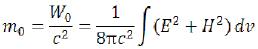 (I-5)
(I-5)
or it is more evident, for physics: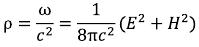 (I-6)
(I-6)
Here we have also approached gravitation of elementary particles and her source.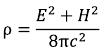 (I-7)
(I-7)
According to the law of universal gravitation, the small weight (dm) creates around itself (in the point remote from a gravitation source on r distance) gravitational field intensity:
But, according to physics, the size of this weight is defined as: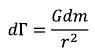 (I-8)
(I-8)
And ρ we have calculated density earlier, then the equation of the gravitational field intensity created by an elementary particle in surrounding space in a differential form (it is a form of record of the equation, but not a form of the field existence) will register: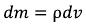 (I-9)
(I-9)
The equation of the gravitational field intensity created by an elementary particle can be written down also in an integrated form: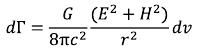 (I-10)
(I-10)
Here one feature of physics has come up. As force is a size vector, she should be integrated by rules of the vectors addition in each point. Replacement of the vector sum with her scalar equivalent will give a mistake, especially in a near zone. The laws of the nature are shouldn’t substitute the reasons of symmetry.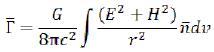 (I-11) Gorunovich equation of gravitation
(I-11) Gorunovich equation of gravitation
This a small formula, is very capacious for physics, will send not one fantastic “theory” of gravitation to archive of history of the physics development, having caused anger of their authors who have got a false idea that their opinion and mathematical formulas are higher than laws of the nature. Here are operate laws of the nature: when it is necessary - include when it isn’t necessary - disconnect, substituting it instead of the science. Here only the nature doesn’t submit to it.
The equation (I-11) can be written down also in more habitual form, having substituted in it (I-7)
As we see, the received gravitation equation - it is the vector equation, differs from standard (in which the vector is taken out for a sign of integration), on the basis of which any mathematical fairy tale has been constructed.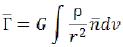 (I-12) - the gravitation equation
(I-12) - the gravitation equation
We will sum up the result. We, strictly working within laws of the nature, have received the equations for the rest mass of an elementary particle and created by the based elementary particle of a gravitational field, the theories of gravitation of elementary particles which have become a basis. - It is action within SCIENCE. And fictional quarks and fantastic Higgs boson have appeared out of work.
1.3. The choice of the units system
When I on the website “Wikiznanie” in the article “Intensity of a Gravitational Field”, the section “Intensity of a Gravitational Field and Field Theory of Elementary Particles” have given only four formulas from given above (No.: I-7, I-10, I-11, I-12), I have received the following:
“To attention of experts: formulas (...) aren't true, correction is required”.
“The SI system electric field (E) has dimension of volts on meter, and intensity of a magnetic field (H) - amperes on meter. And you mix them in one line so as if it is sizes of one physical dimension. Correct please. Fedosin”
It is about the equations following from the equation (I-3) - consequences of the law of conservation of energy.
So what should be trusted: to the fundamental law of the nature - to the Law of conservation of energy or the International units system (SI) accepted now? Which of them misleads?
According to the Law of conservation of energy, in the equation (I-3) we have put density of two types of electromagnetic energy - and the energies are summarize. If we multiply each of equation elements by identical coefficient of dv, dimensional volume - we will receive addition of two types of electromagnetic energy: electric and magnetic:
as: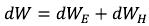 (I-13)
(I-13)
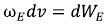 (I-14)
(I-14)
The electrodynamics describing electromagnetic fields including claims the electromagnetic fields created by elementary particles that according to laws of electromagnetism, intensity of electric field can be transformed to intensity of a magnetic field (as arises at the movement of electric field). Therefore: the equation (I-3) is lawful, according to Classical electrodynamics and the law of conservation of energy, and is RELIABLE.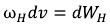 (I-15)
(I-15)
The law of conservation of energy is disappears - is remain a SI.
The sizes possessing different dimension can't be put, but it is possible to multiply - here only that we then will receive. We will take a case of the variation electromagnetic field with f frequency. If to multiply E and H something will turn out, dimension of volts-ampere/metr2, disappearing and reviving again with a frequency 2f (it will be nullified every time when E or H is equal to zero). - Something reminds the Quantum theory with her Fairy tales. But the volt-ampere is a stand-alone unit of measure of full capacity, by definition, equal “full capacity of an electric chain with the single-phase sinusoidal alternating current proceeding on her at the operating (effective) values of voltage of 1 V and current 1 A” (the quote from Wikipedia). Having divided volt-ampere on metr2, we will receive unit of full capacity divided per unit area (characterizes ability of material, or contact, to transfer, or to pass, electric power). From the point of view of electric chains and SI - it is normal.
To put sizes of different dimension, it is necessary to increase each of them by the corresponding coefficient to lead them to uniform units. But it is so possible to put any physical quantities: the mathematics will bear it, here only the PHYSICS will disappear, and in the equation (I-3) the Law of conservation of energy - the fundamental law of the nature, such unloved has been written down by the Quantum theory.
Perhaps having changed an original picture of a microcosm for display it through points with filters of the International units system (SI), the physics of the second half of the 20th century has also rolled down to the world of the mathematical FAIRY TALES issued for SCIENCE.
Here therefore, I have also stopped on checked by time (opponents will call “outdated”) to the units system of Gaussian unit system on the basis of which many equations of Electrodynamics - SCIENCES have been written. And to translate the equations after they have been received, in other the units system, everyone can independently make if of course he has the corresponding knowledge which would be desirable for having.
1.4. Introduction to the gravitation theory of elementary particles - a result
I, extremely in detail, have proved the equations of the gravitation theory of elementary particles. All this is obvious and elementary things. Any, knowing physics, can be convinced in truth of the presented equations.
Gravitation theory of elementary particles
As all bodies in the Universe consist of elementary particles, except of course fantastic (dark matter and other representatives of mathematical fairy tales), conclusions from this theory will have global value. The developed theory isn’t relativistic as in elementary particles the special theory of relativity (STR) doesn’t work.
2. The gravitational field of an elementary particle with quantum number L>0 (except a photon)
The field theory of elementary particles, having established an electromagnetic structure of elementary particles, I have determined by that the gravitation nature as ability of the electromagnetic fields energy to an attraction.
According to the law of universal gravitation, classical electrodynamics, the field theory of elementary particles (in abbreviated form the field theory) and Einstein’s formula, a gravitational field intensity of the based elementary particle is equal:
where G - is a gravitational constant, E - is the electric field intensity of an elementary particle (both constant, and variable), H - is the magnetic field intensity of an elementary particle (both constant, and variable), with - the velocity of light, R - is the distance from a supervision point to a point of integration, n - is a single vector from a supervision point in an integration point.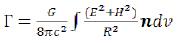 (1)
(1)
Lack of anti-gravitation in the nature follows from the equation (1). By what don’t do E or H, and the sum of their squares will ALWAYS be positive, except for of course fantastic “theories”, but to the physicist those don’t interest.
But in practice, it is difficult to use the equation (1) as it is required to know the sizes E and H in each point of space. The field theory helps to overcome this difficulty. We will start.
Let us should solve a problem of finding of the gravitational field intensity created by the based elementary particle. About an elementary particle are known: the size of the rest mass with a set of quantum numbers and other characteristics, location of the center, orientation a back.
We will place the beginning of coordinates in the center of an elementary particle, and we will direct axis Z along a vector a back. Then, according to the field theory of elementary particles, the ring area of rotation of the variable electromagnetic field of an elementary particle will lie in the plane (X, Y), and the center will coincide with the beginning of coordinates. Coordinate (Z) will mean height of an arrangement of a required point over the plane (or under the plane when Z is less than zero). The weight which is contained in the variable electromagnetic field will rotate on the average radius of r0~, determined by the field theory. As the radius of rotation is replaced with an average, we can instead of volume distribution of substance in ring area use linear, having avoided, on the one hand, difficult integrals, and on the other hand, considerable losses of accuracy, at determination intensity of a gravitational field outside ring area.
So, let we have a thin material thread, the mass of m0~ and radius r0~, placed in the plane (X, Y) with the center at the beginning of coordinates (see rice 1). We will consider other part of the rest mass (m0) of an elementary particle (we will call it m0=) later. In a distant zone of weight will develop and will yield right result, and in a near zone it will allow to minimize a deviation (from the real field).
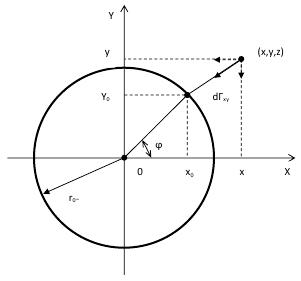
Fig. 1 Approximation of ring area of an elementary particle
According to the field theory of elementary particles:
where L - is the main quantum number of an elementary particle in the field theory, ħ - is the Plank constant divided on 2π, k~ - is the coefficient specifying what part of total internal energy of the based free elementary particle is concentrated in her variable electromagnetic field.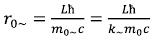 (2)
(2)
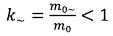 (3)
(3)
Where m0= - is the weight size concluded in constant fields (electric and magnetic) the based free elementary particle. For the elementary particle which is a part of an atomic nucleus, this size will be size defects less than the mass of a particle, the corresponding binding energy of a kernel.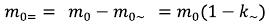 (4)
(4)
The linear substance density (σ) in ring area of an elementary particle:
We will determine coordinates of the integration point of ring area of an elementary particle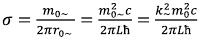 (5)
(5)
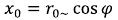 (6)
(6)
where ϕ - is a corner between axis X and a vector from a point of the beginning of coordinates in integration point (x0, y0, 0).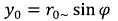 (7)
(7)
Distance from a point (x0, y0, 0) to a point (x, y, z) will be:
The segment mass of ring area is creating a gravitational field will be: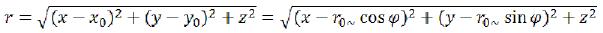 (8)
(8)
And the size of the gravitational field intensity created by him in a point (x, y, z):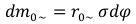 (9)
(9)
For further integration we will spread out dГ~ vector to components. dГ~ projection on the plane (X, Y) it is equal: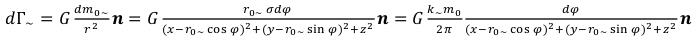 (10)
(10)
DГ~ projection on axis Z: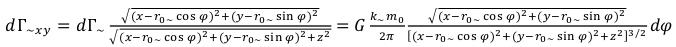 (11)
(11)
DГ~ projection on axis X: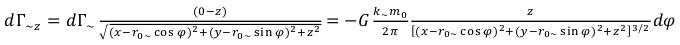 (12)
(12)
DГ~ projection on axis Y: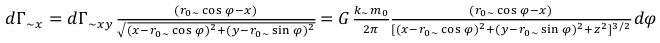 (13)
(13)
Now it is possible to carry out integration: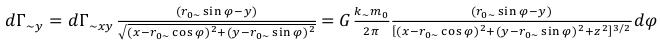 (14)
(14)
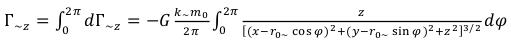 (15)
(15)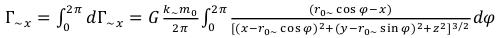 (16)
(16)
We introduce one more designation. The ring area radius of an elementary particle: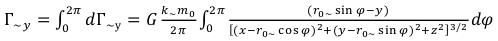 (17)
(17)
We will note that r is a distance from the center of ring area to a point in which intensity of the field (x, y, z), is defined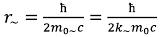 (18)
(18)
The equations (15)-(17) are fair outside the ring area (when r > r~) creating the basic (more than 90%) a gravitational field of an elementary particle, limited to r~ radius (fig. 2 see). But there is still an area of space in ring area (when r < r~) creating a gravitational field. We will consider as well this area of space.
So, we look for intensity of the gravitational field created by substance with an average ρ0~ density in a ring with r~ radius. In fig. 2 the cross section of an elementary particle is displayed (in the plane (X, Z)) when the plane is carried out through a supervision point. As the ring area of an elementary particle has the central symmetry, and also symmetry in relation to axis Z, we can use it and simplify a task. We will solve a problem on the example of protons and neutrons as in them more than 99% of mass of substance are concentrated.
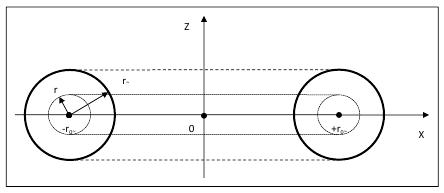
Fig. 2 the Cross section of an elementary particle, with quantum number L=3/2 (a proton, a neutron)
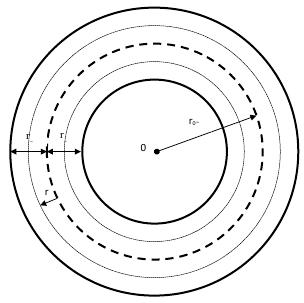
Fig. 3 Ring area of an elementary particle, with quantum number L=3/2 (a proton, a neutron). The top view which is a little reduced.
According to the second of the Pappus - Guldin theorems, the volume of the geometrical figure formed by rotation of a circle with r~ radius around the center of an elementary particle will be:
From here it is possible to determine average density (ρ0~) as the relation of the weight concentrated in the variable electromagnetic field of an elementary particle to the volume occupied by her: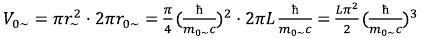 (19)
(19)
According to the first theorem of the Pappus-Guldin theorems, the surface area of rotation is equal to the length work of the rotating line at length of a circle as which radius serves the distance from an axis to a line barycenter. For the gravitational field created by the variable electromagnetic field of an elementary particle, length of the line will be equal in our case 2πr~, and circle length 2πr0~.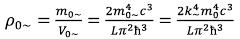 (20)
(20)
Now it is possible to define the gravitational field intensity arising on a surface of the area occupied by the rotating variable electromagnetic field she will be: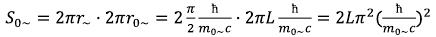 (21)
(21)
The vector will be perpendicular surfaces and is directed to a source. As we see, the size of the gravitational field intensity created by the variable electromagnetic field of an elementary particle on a surface of ring area in which the field rotates is proportional to a cube of size of the rest mass.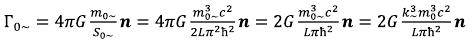 (22)
(22)
Having substituted in (22) known the rest mass of a proton, the calculated parameter k~ (0.9221), quantum number L (3/2), and others, we will receive the size approximately equal to the maximum intensity of a gravitational field of the free based proton:
At a neutron a little big size will turn out: 9.5 • 10-7 m/sec2, and at the based electron: 4.8 • 10-16 m/sec2. Exact values can be defined by a formula (45), they will differ from presented less than for 1 percent. I hope, the level of influence of gravitation on a microcosm is well visible.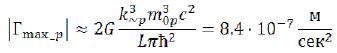
For the determination of the gravitational field intensity in ring area of an elementary particle (see fig. 2), we will use the Pappus-Guldin theorems again. The volume of the geometrical figure formed by rotation of a circle with r radius (smaller, than r~) around the center of an elementary particle, will be:
and her surface area: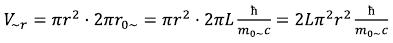 (23)
(23)
The average weight concluded in volume of V~r will be: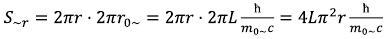 (24)
(24)
From where, the gravitational field intensity arising on a surface of a geometrical figure will be: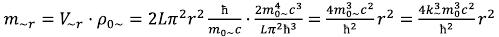 (25)
(25)
where n - is a single vector, perpendicular surfaces of a geometrical figure.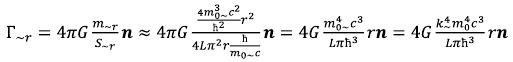 (26)
(26)
The vector is perpendicular surfaces and is directed to a source. As we see, at aspiration of r to zero, the gravitational field intensity created by the variable electromagnetic field of an elementary particle will aspire to zero.
The elementary particle has one more source of a gravitational field: m0= - is the weight concluded in constant electric and magnetic fields of an elementary particle. We will divide her into three parts:
where:
According to classical electrodynamics and Einstein’s formula, m=0 it is equal:
Where Em - that is the maximum intensity of constant electric field of an elementary particle on a surface of ring area. For a constant magnetic field of the loaded elementary particles it is possible to enter similar to Hm and to simplify expression, but for a magnetic field of neutral elementary particles it won’t turn out - there more difficult structure of the field.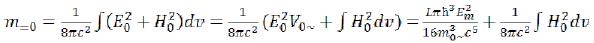 (27)
(27)
For simplicity of record of the equations, we introduce one more coefficient:
where k=0 - the coefficient (size about 0.001) indicating the part of the rest mass of an elementary particle concentrated in ring area in a constant electric and constant magnetic field.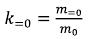 (28)
(28)
For the gravitational field created by this part of mass of a constant electric and magnetic field we will receive the result similar (15)-(17),
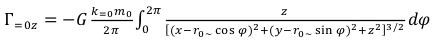 (29)
(29)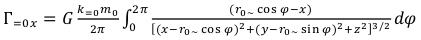 (30)
(30)
Similarly in a near zone it is necessary in (26) to replace one m0~ with m=o: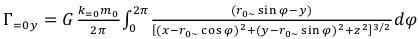 (31)
(31)
We can put the similar equations and we will receive expressions for part of the rest mass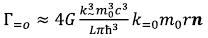 (32)
(32)
The sizes m=e and m=m can be determined, knowing in each point of space of the size E and H (for this purpose it is necessary to use the field theory of elementary particles).
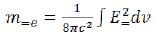 (33)
(33)
But for definition of the rest of a gravitational field of an elementary particle, it isn’t obligatory to do it. It is possible to enter density of electromagnetic substance (ρ=) the sums constant of electric and magnetic fields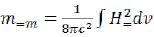 (34)
(34)
Then, according to the law of universal gravitation, we will receive a vector of the gravitational field intensity created ρ=: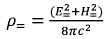 (35)
(35)
where (x0, y0, z0) - coordinates of a point of a source, the considered gravitational field, (x, y, z) - supervision point coordinates.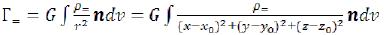 (36)
(36)
But it are required for us making Г=. The size of a projection of Г= on the plane (X, Y) it is equal:
Projection of Г= on axis Z: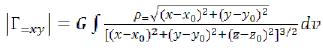 (37)
(37)
Projection of Г= on axis X: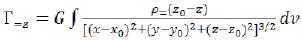 (38)
(38)
Projection of Г= on axis Y: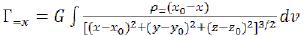 (39)
(39)
It is time to put components of vectors of the gravitational field intensity. For a gravitational field of an elementary particle, outside ring area we will have: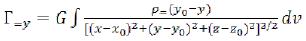 (40)
(40)
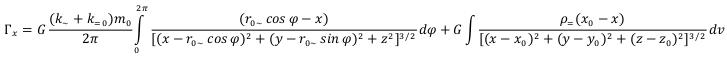 (41)
(41)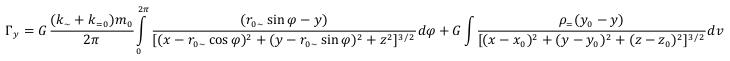 (42)
(42)
And the size of a vector of the gravitational field intensity will be: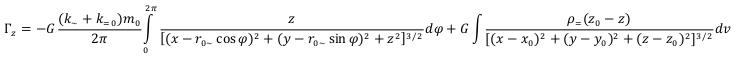 (43)
(43)
For a gravitational field of an elementary particle, in ring area we will have: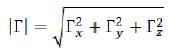 (44)
(44)
The mathematical expressions having a little general with a formula of the gravitational field intensity of dot gravitational object have turned out: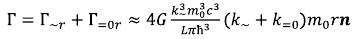 (45)
(45)
on the basis of which, many mathematical fairy tales have been created.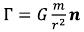 (46)
(46)
If in the equations (41)-(43) to put r0=0 (field of the dot object which is not existing in the nature), then the semblance will turn out (46):
But it is only part of a gravitational field. There still will be a gravitational field created by a constant electric and constant magnetic field of an elementary particle out of ring area, and this field extends in infinity, under laws of classical electrodynamics.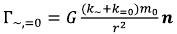 (47)
(47)
Now we will deal with symmetry which is possessed by a gravitational field of an elementary particle.
The formulas 41 - 43 follows from the equations that the gravitational field of an elementary particle won’t change if to change particle backs for opposite. For elementary particles with zero to backs it belongs to change of the direction of a vector of the internal rotary moment, on opposite. At any other change of orientation of an elementary particle also her gravitational field will change. Therefore: the gravitational field of an elementary particle doesn’t possess spherical symmetry.
But the gravitational field of an elementary particle remains symmetric concerning the straight line passing through the center of an elementary particle and perpendicular plane of rotation of the variable electromagnetic field (parallel or anti-parallel to a vector of the internal rotary moment). I.e. the size of the gravitational field intensity of an elementary particle is identical to all points equidistant from the center of an elementary particle and, along with it, equidistant from a symmetry axis. - The structure of elementary particles is reflected in structure of their fields.
It is possible to invent many mathematically beautiful theoretical constructions, but the gravitational field of substance is created by elementary particles of which it finally consists.
3. The gravitational field of ring area
We will consider a case of some distribution of weight in ring area of the variable electromagnetic field (other than constant density). Let density will be equal ρ~(x).
Then the weight size (dm~r) which is contained in a ring segment of radius x and dx thickness
In this case, the weight concluded in volume of V~r will be: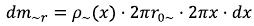 (48)
(48)
Then the equation (26) will correspond, and the gravitational field intensity arising on a surface of a geometrical figure will be: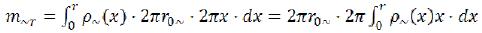 (49)
(49)
We have received replacement of the equation (26) for a case of some distribution of the substance density in the variable electromagnetic field of an elementary particle, in ring area. In this case the equation (45) for components of the gravitational field intensity of an elementary particle created by electromagnetic fields of internal area of radius of r on a surface of a geometrical figure in ring area will also correspond: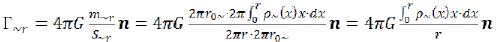 (50)
(50)
and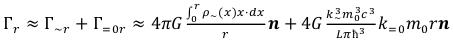 (51)
(51)
where E~ - is the intensity of variable electric field of an elementary particle, H~ - is the intensity of a variable magnetic field of an elementary particle.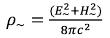 (52)
(52)
Isn’t necessary on the equation (51), seeing 1/r, to cost any fantastic theories about "strong" gravitational fields in elementary particles. Here just the physics and when you substitutes distribution (52) in integral works - euphoria will thaw, and the gravitational field will become just gravitational field again.
Now there is a little mathematics.
We will allocate from the equation (26) m~r/S~r and we will paint it.
where Sr - is the area of a circle of radius of r, lr - is the circle length of r radius. We won’t reduce it further, and we will stop on it. Then the equation (26) can be rewritten: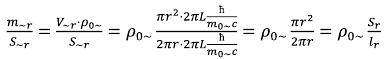 (53)
(53)
Persons interested can be convinced (having painted further) that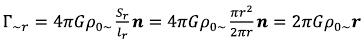 (54)
(54)
Where the r-vector is directed to a source of a gravitational field, as well as is the n-vector.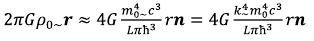 (55)
(55)
I.e. the Pappus - Guldin theorem having reduced circle length, I have transferred a problem of finding of a gravitational field in ring area of an elementary particle from three-dimensional option to two-dimensional option that simplifies integrals and facilitates her decision.
Now we will solve one mathematical problem. Let us have a thin ring, thickness of dr, average radius r0 and mass of mk. We will look what gravitational field it creates outside and inside. We will place a ring in the plane (X, Y) with the center at the beginning of coordinates (see fig. 4).
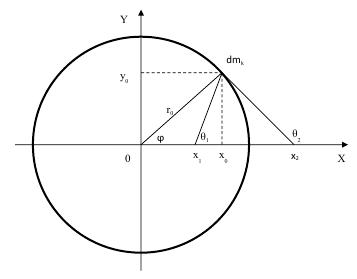
Fig. 4 Thin ring
where:
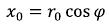 (56)
(56)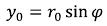 (57)
(57)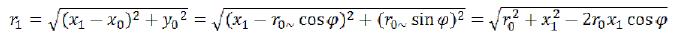 (58)
(58)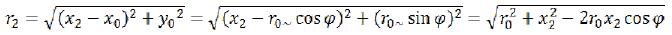 (59)
(59) (60)
(60)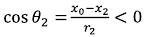 (61)
(61)
r1 and r2 - are the distances from dmk to x1 and x2 respectively, dϕ - is the angular size of the considered segment.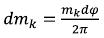 (62)
(62)
The size of the gravitational field intensity created by the dmk segment in two-dimensional space in a point (x, 0) will be:
dГ projection to axis X for points of x1 and x2, will be: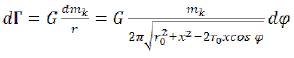 (63)
(63)
And the projection to axis X of the gravitational field intensity created by a thin ring will be: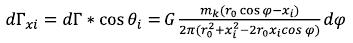 (64)
(64)
In a point of xi=r0 the difference of two infinity - not a physical case turns out, in the nature there are no infinitely big fields.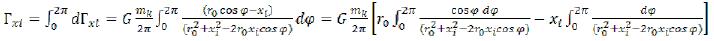 (65)
(65)
We introduce designations:
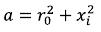 (66)
(66)
The first integral can be transformed and reduced to the second: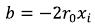 (67)
(67)
Then contents of a square bracket of the equation (65) will correspond: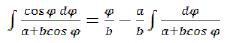 (68)
(68)
At long distances when xi > > r0 turns out: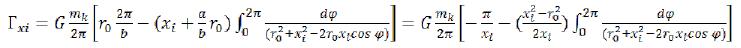 (69)
(69)
as had to be for a gravitational field of the infinitely long cylinder. The second member of a square bracket gives-π/xi on infinity and that will be in a near zone, at small distances - we will look.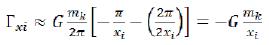 (70)
(70)
We will paint it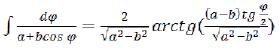 (71)
(71)
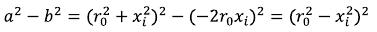 (72)
(72)
Then: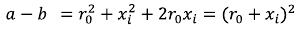 (73)
(73)
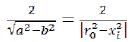 (74)
(74)
We will substitute it in (71), we will receive: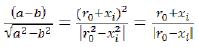 (75)
(75)
Then the equation (69) will correspond: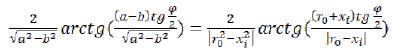 (76)
(76)
If to substitute in him ϕ=2π, we will receive that intensity of a gravitational field in a ring (in any point) is equal to zero, and outside of a ring is equal - Gmk/R. The thin material ring, dr thickness, has created a gravitational field, intensity Гxi in each point (i) of space, outside a ring. The relation of the size change of the gravitational field intensity to the size of distance on which this change has happened is called a gradient. In our case (for a source of a gravitational field), we will have: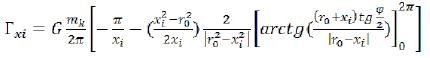 (77)
(77)
We will paint mk. We introduce substance density (σ). Then: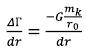 (78)
(78)
Then (78) will correspond: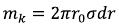 (79)
(79)
I.e. the gravitational field intensity in a source of gravitation is created by the substance density (his electromagnetic field). In three-dimensional space it will be similar, only 2π (a full corner of a circle) it will be replaced on 4π (a full space angle of the sphere), and area density (σ) will be replaced with volume density (ρ).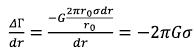 (80)
(80)
But the gradient from mathematical function is equal to her first derivative, and then the gradient of the gravitational field intensity in ring area of an elementary particle (a scope of the equation 51) will be:
In the equation (81) the last two (negative) members point to sources of gravitation of an elementary particle (the variable electromagnetic field and a constant electric and constant magnetic field), and the first (positive) member reflects feature of distribution of the field in space, ρ~ - is defined in (52).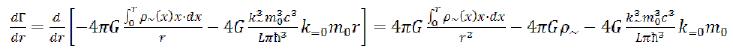 (81)
(81)
In the nature there are no dot sources of gravitation - the gravitational field is created by the electromagnetic field distributed in space. And as electromagnetic fields submit to laws of electromagnetism, the same laws also influence structure of the created gravitational field. Having placed an elementary particle in a constant external electric or magnetic field, we will change structure of her constant electromagnetic fields and consequently and the gravitational field created by them.
In the nature there is also no uniform substance. Each atom of substance consists of a massive kernel and electrons of a cover, and each kernel has a certain structure and consists of the protons with neutrons which aren’t spherical educations. Having evenly smeared atom on the space occupied by it, we lose a gravitational field of a center (which energy is the main part of energy of a gravitational field of elementary particles of atom), and mathematical fairy tales begin then.
4. The gravitational field created by an annular domain of the free not moving elementary particle beyond its limits
Thanks to symmetry of a gravitational field, equation (41) - (42) it is possible to simplify. We introduce new designation:
Then the equations (41) and (42) can be rewritten for the points equidistant from the center of an elementary particle: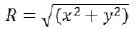 (82)
(82)
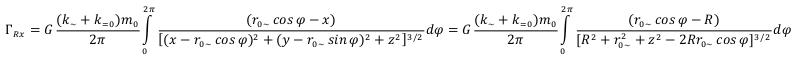 (83)
(83)
As we see, certain integrals from (83) and (84) are equal, then, having chosen one of them, we will receive: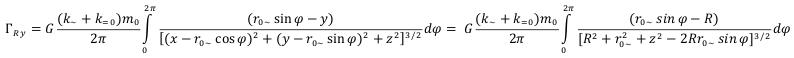 (84)
(84)
where nR - is the single vector lying in the plane parallel to the plane of the elementary particle passing through a point of supervision (R) and directed towards an axis, the perpendicular plane and the elementary particle passing through the center. Similarly it will turn out also a component Z from (43):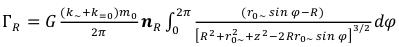 (85)
(85)
And the equation (44) a little will change: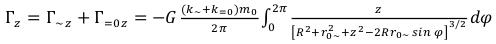 (86)
(86)
As we see, having put in (86) z=R, we will receive result, excellent from (85) - the gravitational field of an elementary particle isn’t spherically symmetric. It is still obvious that the received equations (85) and (86) don’t correspond to the equation (46), but are reduced to that if to put r0~ = 0 - but we then will lose a natural source of a gravitational field (81) and we will replace him fantastic.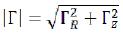 (87)
(87)
We will look what intensity of a gravitational field on the axis passing through the center of an elementary particle and its perpendicular plane (R=0) is equal to. Then the integral (85) will correspond:
As a certain integral from 0 to 2π both a sine, and a cosine, will give zero - a component of a gravitational field, created by each elementary segment, has been compensated the component a gravitational field, created by a similar symmetric segment.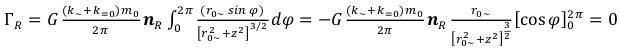 (88)
(88)
And here the equation (86) will yield result, other than zero:
And only in the center of an elementary particle intensity and this components of a gravitational field will give zero too.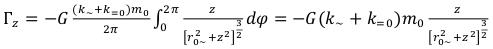 (89)
(89)
The equations (85) - (89) describe a gravitational field of the free based elementary particle without the gravitational field created by constant electric field and a constant magnetic field outside ring area, and these are more than 95% of all gravitational field. For the accounting of other part of a gravitational field, it is necessary to use the following integrals from (41) - (43):
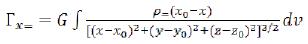 (90)
(90)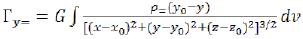 (91)
(91)
And then, addition not of scalar sizes, but vectors: ГR, Гz, Гx=, Гy=, Гz=.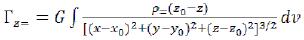 (92)
(92)
So, we have received the equations of the gravitational field intensity created in the nature by the free based elementary particle. Having placed an elementary particle in an atomic nucleus, we will change her constant electromagnetic fields, and, therefore, and the gravitational field created by this particle. As appears from (85) and (86), intensity of a gravitational field of an elementary particle depends also on orientation her back. In the developed theory there was no place for fantastic: gravitons, gravitino and Higgs boson - they aren’t necessary to the nature, except for the vector meson nicknamed “Higgs”. The gravitational field of substance is created by electromagnetic fields of elementary particles of which this substance consists what the physics has ingeniously guessed hundred years ago, but only today it can approve it!
5. Components of the gravitational field created by ring area of the free not moving elementary particle beyond her limits
We will define intensity of a gravitational field in the plane of an elementary particle. The equation (86) will give zero, and here the equation (85) will yield more interesting result.
If in denominators of integrals in (93) it was possible to replace sin ϕ with its average value in the range of 0 - 2π (i.e. on zero), then integrals sharply would become simpler: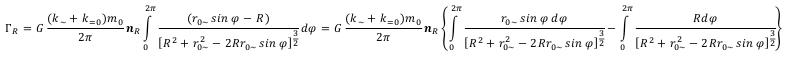 (93)
(93)
where R - is distance from a supervision point to the center of an elementary particle, and r0~ - is the radius of an elementary particle in the field theory, is defined in (2). I remind that a certain integral from a sine in the range of 0 - 2π gives zero.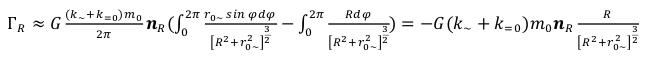 (94)
(94)
We have received the expression similar (89) saying that in a gravitational field of an elementary particle there is spherically a symmetric component. The most interesting in (94) is the fraction denominator at which there is a square of radius of an elementary particle from the field theory of elementary particles (lying in the base of the developed theory of gravitation together with Einstein’s formula and the law of universal gravitation) - the nature limits a gravitational field.
We introduce new designation:
For a gravitational field outside an elementary particle β will be less than 1, and at long distances to aspire in zero. Then the equation (93) will correspond: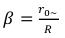 (95)
(95)
The uncertain integral from the sub integral function similar (96), according to the Internet to a resource (http://matematikam.ru/), has the following decision: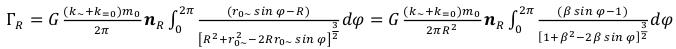 (96)
(96)
The equation (96) can be painted, it will turn out: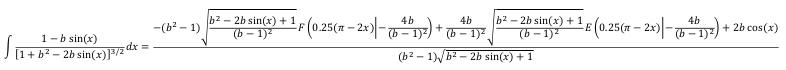 (97)
(97)
Can seem that the analog of the equation (46) has turned out, but it is illusion: in everyone β, it agrees (95), there is R and rejection of this fact leads to mathematical manipulations over laws of the nature.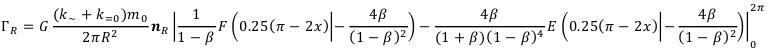 (96-2)
(96-2)
In figure 5 the family of curves of sub integral function (97) is presented, at the fixed values β (0.5, 0.25, 0.1, 0.05, 0.025, 0.01), received with the help the Internet of a resource (http://www.yotx.ru/). To bigger value β there is corresponds the big size of a maximum on graphics.
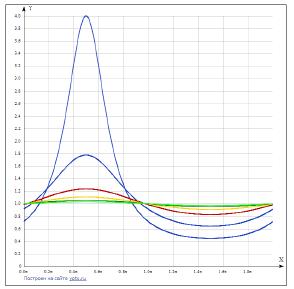
Fig. 5 is the family of curves of function (97) in the range of integration of 0 - 2π.
As we see, a certain integral from any of curves will give the value exceeding 2π that together with (89) tells about existence in a gravitational field of an elementary particle spherically symmetric component, defined:
Even for spherically components of a gravitational field of an elementary particle, the mathematical expression differing from (46) has turned out symmetric.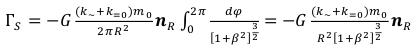 (98)
(98)
Besides, in a gravitational field of an elementary particle is available also asymmetric a component, determined by structure of her electromagnetic sexes which are defined as:
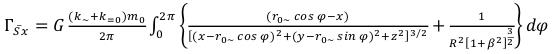 (99)
(99)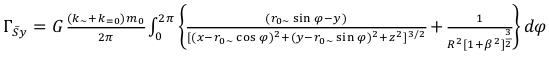 (100)
(100)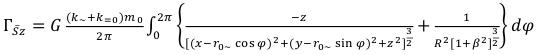 (101)
(101)
6. The gravity potential of the field created by ring area of the free not moving elementary particle beyond her limits
In physics there is such concept as gravitational potential (ϕ): “the scalar function of coordinates and time characterizing a gravitational field in classical mechanics equal to the relation of potential energy of a material point (in a gravitational field) to the mass of this point”. Knowing intensity of a gravitational field in any his point, it is possible to determine also the gravitational potential of some point of the field as:
We will take integral from symmetric components (98):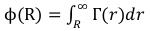 (102)
(102)
as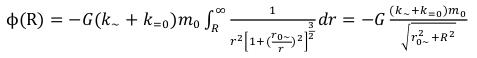 (103)
(103)
As we see, even received in (103) expression, for symmetric components of a gravitational field of an elementary particle, differs from standard: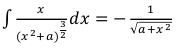 (104)
(104)
and on the basis of (105) have composed “theory” about black holes and frighten by them all.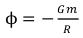 (105)
(105)
What then to tell about all gravitational field of an elementary particle which isn’t even spherically symmetric.
Gravitational capacity of the field created by ring area in a point with coordinates (x, y, z), under a condition (x2+y2= Ɩ2) is defined as:
For determination of gravitational potential of all gravitational field of an elementary particle, it is necessary to consider still and the gravitational field created external by a constant electric and constant magnetic field. And what the general result - obviously wouldn’t turn out that it will be excellent from (105).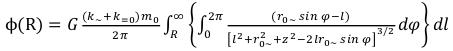 (106)
(106)
In conclusion of the first part I will tell: in the twentieth century in physics there was a set of the theoretical constructions called by authors “theories of gravitation”. Over time the physics will give them the assessment, but whatever authors of these hypotheses spoke, and gravitational fields in the nature are created by elementary particles of which substance consists. All other gravitational fields are an imagination product - mathematical fairy tales, and existence in the nature of other forms of gravitation (instead of the existing electromagnetic form) should be not postulated, and to prove.
7. Nature of inertial properties of elementary particles
The field theory of elementary particles, having established an electromagnetic structure of elementary particles, I have determined by that the gravitation nature, having confirmed existence in the nature of an electromagnetic form of gravitation. But if electromagnetic matter creates around itself gravitation, i.e. electromagnetic weight is gravitational, and then there is one more question: whether electromagnetic weight is a source of inertia of elementary particles. We will deal with this question.
Let in some elementary volume of space of dv there is uniform electric field intensity of E.
According to Classical electrodynamics, his energy will be:
And according to Einstein’s formula, this field will have weight: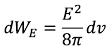 (107)
(107)
and this weight is will gravitational - is create around itself a gravitational field.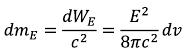 (108)
(108)
We will deal with its inertial properties now.
Let at us, in some inertial reference system, the elementary particle was based, and at some point time was known to us her electric and magnetic field (to us the vector of intensity of electric field (E) and a vector of intensity of a magnetic field (H) are known). In this reference system we can define total internal energy of the electromagnetic field and size of his weight. Now we will pass to other inertial reference system (will call her shaded) moving in relation to the previous reference system with a constant speed of V along an axis x. To determine new sizes of vectors of intensity (E, H) we will use Lorentz’s transformation for an electric and magnetic field:
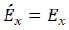 (109)
(109) 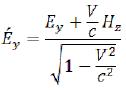 (110)
(110) 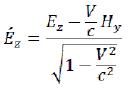 (111)
(111)
At speeds, it is much lower than the velocity of light (V < < c), these expressions will become simpler: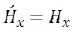 (112)
(112) 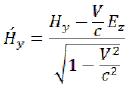 (113)
(113) 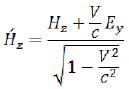 (114)
(114)
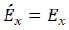 (115)
(115) 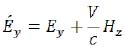 (116)
(116) 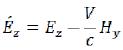 (117)
(117)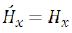 (118)
(118) 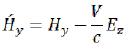 (119)
(119) 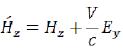 (120)
(120)
The last six equations can be presented in a vector form:
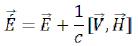 (121)
(121)
According to the equation (122) moving electric field generates a magnetic field. As the based elementary particle had own magnetic field (H), this field (122) develops by rules of addition of vectors. We will designate the additional member as ΔH: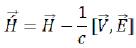 (122)
(122)
The new vector will be result of addition of vectors. Let the corner between initial vectors be equal α, then: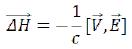 (123)
(123)
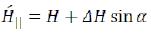 (124)
(124)
where: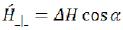 (125)
(125)
θ - is a corner between vectors of V and E.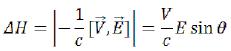 (126)
(126)
The square of intensity of a resultant magnetic field will be:
as the squares sum of a sine and cosine is equal to unit.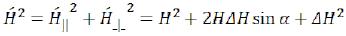 (127)
(127)
When averaging in the directions, the second member of the equation will give zero therefore we will receive:
Having divided (128) on 8π, we will pass to energy density. I remind that in the Gaussian unit system (used in electrodynamics) intensity of an electric and magnetic field have identical dimension.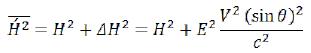 (128)
(128)
According to Classical electrodynamics, energy of such magnetic field will be:
As we see, energy density, in comparison with the based particle, I have grown by size: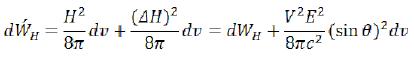 (129)
(129)
Now we will substitute in the received equation (108), we will receive: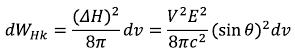 (130)
(130)
Having taken a certain integral on all electromagnetic field of an elementary particle, we will receive for electric field components: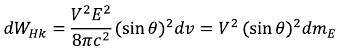 (131)
(131)
And respectively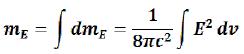 (132)
(132)
It has turned out that electric a component of electromagnetic mass of an elementary particle has inertial weight.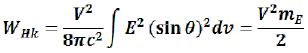 (133)
(133)
But the electromagnetic field has also a magnetic component. Persons interested can repeat made and for a magnetic component. And it is simpler to compare the equations (121) and (122) and to remember that vector develop by rules of addition of vectors, and the sign “-“ in (122) won’t change the size of a square orthogonal field components which defines additional energy of the field. Therefore, and for a magnetic component of the electromagnetic field of an elementary particle, it is possible to write down:
And respectively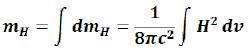 (134)
(134)
From Classical mechanics we know that kinetic energy of the inertial mass of m moving with a speed of V is equal: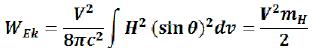 (135)
(135)
In our case, kinetic energy of the electromagnetic field of an elementary particle is equal: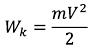 (136)
(136)
Therefore: an electric and magnetic component of the electromagnetic field of an elementary particle also is creating inertial properties of field matter of which Universe substance consists. For moving of such field weight or giving of speed to it, it will be required to apply force, as in Classical mechanics.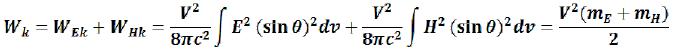 (137)
(137)
So, in the first part of the gravitation theory of elementary particles it has been established that the electromagnetic mass of the electromagnetic field of elementary particles creates their gravitational fields. Now it is established still that the electromagnetic mass of the electromagnetic field of elementary particles creates their inertial properties, according to Classical mechanics. Therefore: weight in elementary particles is electromagnetic by the nature.
We will remember Albert Einstein’s words written to them at the beginning of the 20th century: ”Now we are actually forced to distinguish “matter” and “fields”, though we can hope that the future generations will overcome this dualistic representation and will replace it with uniform concept as the theory of the field of our days vainly tried to make it”. - Hundred years of persistent and dedicated work of several generations of physicists, supporters of the Theory of Paul that this day has come once were required. And in 2015 the New physics - the physics of 21 centuries could claim: “Elementary particles of which Universe substance consists - are a form of electromagnetic field matter”.
Continuation: Gravitation theory of elementary particles Part 2
 Новая_физика - физика_21_века
Новая_физика - физика_21_века



